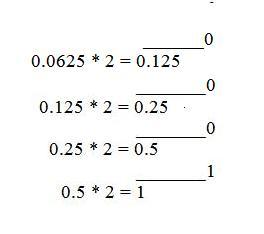MASTER OF COMPUTER APPLICATIONS
Course Code : MCS-012
Course Title : Computer Organisation and Assembly Language Programming
Assignment Number : MCA (2)/012/Assign /2015-16
Maximum Marks : 100
Weightage : 25%
Explain the double precision floating point IEEE 754 representation. Represent the number (124.0625)10 using IEEE 754 single precision and double precision representations.
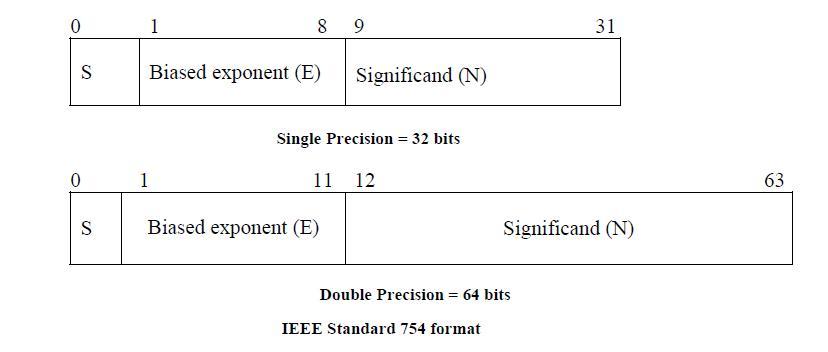
Single Precision
S stands for Sign (white color)
E stands for Exponent (yellow color)
N stands for Number (also called Mantissa or Significand) (green color)
0this Sign bit (1 bit)
1st to 8this Exponent bits (7 bits)
9thto 31this Exponent bits (24 bits)
Double Precision
S stands for Sign (white color)
E stands for Exponent (yellow color)
N stands for Number (also called Mantissa or Significand) (green color)
0this Sign bit (1 bit)
1st to 11this Exponent bits (10 bits)
12thto 63this Exponent bits (53 bits)
First of all to represent we have (63.125)10 using IEEE 754
Since number is a positive number
Sign bit is: 0
| 0 |
Now let’s work on Mantissa part
Convert 124 into binary form i.e 1111100
Remaining is fraction part 0.0625
Now we multiply fraction value with 2 till we get whole number 1 at the end.
We reach 1 so we stop
Write number from top to bottom
We get 0.0625 = 0001
Number (124.0625)10 = (1111100.0001)2
Convert Binary number to Exponent Form
1111100.0001 Will be 1.1111000001 * 26
Discard 1.
Take 1111000001 as Significand
Significand number = (1111000001)2
Significand bits are:
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Fill the Significand in the beginning
Rest all fills it with 0’s
We will have
Significand bits are:
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+6 is the Exponent
So we have to subtract it with 127
Exponent = 127+6=132
Exponent number (132)10 = (10000100)2
Discard overflow bit
Exponent bits are:
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Note: we have to discard overflow bit since we have only 7 bits
For Double Precision Only Exponent
+6 is the Exponent
So we have to subtract it with 1023
Exponent = 1023+6=1029
Exponent number (1029)10 = (10000000101)2
Discard overflow bit
Exponent bits are:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Note: we have to discard overflow bit since we have only 11 bits
Significand bits are:
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Significand will only have a change in terms of Zero’s which are added at the end.
For single precision 23-10=13 Zero’s
For double precision 53-10=43 Zero’s