MASTER OF COMPUTER APPLICATIONS
Course Code : MCSL-025
Course Title : Lab Course
Assignment Number : MCA(II)/L-025/Assignment/15-16
Maximum Marks : 50
Weightage : 25%
Write a program in C language that will accept a Graph as input and will generate its Minimum Cost Spanning Tree.
#include <stdio.h>
#define MAXVERTICES 10
#define MAXEDGES 20
typedef enum {FALSE, TRUE} bool;
int getNVert(int edges[][3], int nedges)
{
// returns no of vertices = maxvertex + 1;
int nvert = -1;
int j;
for( j=0; j<nedges; ++j )
{
if( edges[j][0] > nvert )
nvert = edges[j][0];
if( edges[j][1] > nvert )
nvert = edges[j][1];
}
return ++nvert; // no of vertices = maxvertex + 1;
}
bool isPresent(int edges[][3], int nedges, int v)
{
// checks whether v has been included in the spanning tree.
// thus we see whether there is an edge incident on v
// which has a negative cost. negative cost signifies that
// the edge has been included in the spanning tree.
int j;
for(j=0; j<nedges; ++j)
if(edges[j][2] < 0 && (edges[j][0] == v || edges[j][1] == v))
return TRUE;
return FALSE;
}
void spanning(int edges[][3], int nedges) {
// finds a spanning tree of the graph having edges.
// uses kruskal’s method.
// assumes all costs to be positive.
int i, j;
int tv1, tv2, tcost;
int nspanedges = 0;
int nvert = getNVert(edges, nedges);
// sort edges on cost.
for(i=0; i<nedges-1; ++i)
for(j=i; j<nedges; ++j)
if(edges[i][2] > edges[j][2])
{
tv1=edges[i][0]; tv2=edges[i][1]; tcost=edges[i][2];
edges[i][0]=edges[j][0]; edges[i][1]=edges[j][1];
edges[i][2]=edges[j][2]; edges[j][0]=tv1;
edges[j][1]=tv2; edges[j][2]=tcost;
}
for(j=0; j<nedges-1; ++j) {
// consider edge j connecting vertices v1 and v2.
int v1 = edges[j][0];
int v2 = edges[j][1];
// check whether it forms a cycle in the up until now formed
// spanning tree. checking can be done easily by checking
// whether both v1 and v2 are in the current spanning tree!
if(isPresent(edges, nedges, v1) && isPresent(edges,nedges, v2)) // cycle.
printf(“rejecting: %d %d %d…\n”,edges[j][0],edges[j][1],edges[j][2]);
else {
edges[j][2] = -edges[j][2];
printf(“%d %d %d.\n”, edges[j][0], edges[j][1], -edges[j][2]);
if(++nspanedges == nvert-1)
return;
}
}
printf(“No spanning tree exists for the graph.\n”);
}
void main()
{
int edges[][3] = {
{0,1,16},
{0,4,19},
{0,5,21},
{1,2,5},
{1,3,6},
{1,5,11},
{2,3,10},
{3,4,18},
{3,5,14},
{4,5,33}
};
int nedges = sizeof(edges)/3/sizeof(int);
clrscr();
printf(“The spanning tree for the graph is :\n”);
spanning(edges, nedges);
getch();
}
Program Code:
[codesyntax lang=”c”]
#include <stdio.h>
#define MAXVERTICES 10
#define MAXEDGES 20
typedef enum {FALSE, TRUE} bool;
int getNVert(int edges[][3], int nedges)
{
// returns no of vertices = maxvertex + 1;
int nvert = -1;
int j;
for( j=0; j<nedges; ++j )
{
if( edges[j][0] > nvert )
nvert = edges[j][0];
if( edges[j][1] > nvert )
nvert = edges[j][1];
}
return ++nvert; // no of vertices = maxvertex + 1;
}
bool isPresent(int edges[][3], int nedges, int v)
{
// checks whether v has been included in the spanning tree.
// thus we see whether there is an edge incident on v
// which has a negative cost. negative cost signifies that
// the edge has been included in the spanning tree.
int j;
for(j=0; j<nedges; ++j)
if(edges[j][2] < 0 && (edges[j][0] == v || edges[j][1] == v))
return TRUE;
return FALSE;
}
void spanning(int edges[][3], int nedges) {
// finds a spanning tree of the graph having edges.
// uses kruskal’s method.
// assumes all costs to be positive.
int i, j;
int tv1, tv2, tcost;
int nspanedges = 0;
int nvert = getNVert(edges, nedges);
// sort edges on cost.
for(i=0; i<nedges-1; ++i)
for(j=i; j<nedges; ++j)
if(edges[i][2] > edges[j][2])
{
tv1=edges[i][0]; tv2=edges[i][1]; tcost=edges[i][2];
edges[i][0]=edges[j][0]; edges[i][1]=edges[j][1];
edges[i][2]=edges[j][2]; edges[j][0]=tv1;
edges[j][1]=tv2; edges[j][2]=tcost;
}
for(j=0; j<nedges-1; ++j) {
// consider edge j connecting vertices v1 and v2.
int v1 = edges[j][0];
int v2 = edges[j][1];
// check whether it forms a cycle in the up until now formed
// spanning tree. checking can be done easily by checking
// whether both v1 and v2 are in the current spanning tree!
if(isPresent(edges, nedges, v1) && isPresent(edges,nedges, v2)) // cycle.
printf(“rejecting: %d %d %d…\n”,edges[j][0],edges[j][1],edges[j][2]);
else {
edges[j][2] = -edges[j][2];
printf(“%d %d %d.\n”, edges[j][0], edges[j][1], -edges[j][2]);
if(++nspanedges == nvert-1)
return;
}
}
printf(“No spanning tree exists for the graph.\n”);
}
void main()
{
int edges[][3] = {
{0,1,16},
{0,4,19},
{0,5,21},
{1,2,5},
{1,3,6},
{1,5,11},
{2,3,10},
{3,4,18},
{3,5,14},
{4,5,33}
};
int nedges = sizeof(edges)/3/sizeof(int);
clrscr();
printf(“The spanning tree for the graph is :\n”);
spanning(edges, nedges);
getch();
}
[/codesyntax]
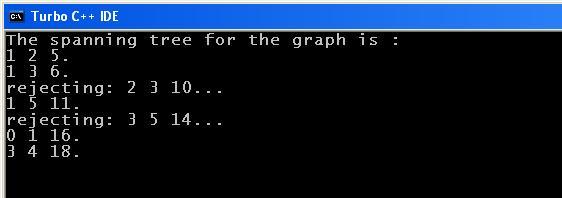
Screen Shots: