Let’s identify variables needed for this program.
In this program, we need to save matrices which consists Rows and Columns. To save this we need Two dimensional ARRAY.
Multi-dimensional Array is a nothing different than any Array but the only difference is that it has more than one dimension to it e.g. square has two dimension and cube has three dimension. The Dimension of array is decided by us in number of square brackets [] selected. If We select two dimension than we have to take two square brackets[][]. It has to be accessed with the help of index number ranging from 0 to n-1 and 0 to m-1. (e.g. num[n][m] will have num[0][0],num[0][1],num[2][2] so on.)
First few variables will be the one which will save the values of matrix with the choice of rows and columns entered by the user and it will be array A[MAX][MAX] and B[MAX][MAX] will be in the form A[M][N] and B[R][S] therefore we will need M,N,R,S will be needed as user decides the row and column of two matrices. Here since we are taking row and column of matrices from the user and hence we can not keep the square brackets empty we will fill that value by maximum value (MAX). This MAX variable will be defined as a constant above the program. Next variable will be array C[MAX][MAX] will be in the form C[M][S] for saving resultant value which will be displayed later. other variables will be I, J and K which will be for FOR Loop so in all TEN variables and ONE constant selected.
The identified variables are A[MAX][MAX],B[MAX][MAX],C[MAX][MAX],I,J,K,M,N,R,S,CH; and identified constant is MAX.
[codesyntax lang=”c”]
#define MAX 15
int A[MAX][MAX],B[MAX][MAX],C[MAX][MAX],I,J,K,M,N,R,S,CH;
[/codesyntax]
Now, Selection of data type is int data type due to the values expected are decimals and they will be holding smaller values so int data type is sufficient.
Best Loop for such kind of condition is FOR Loop the value of loop will start with 0 to M-1. Now here we need nested loop one loop inside the other. So that we can access all the elements with it. In each Case we will need First two nested loops for scanning required array values of Two matrices. Next nested loop will be nested with three FOR loop for multiplication or addition or subtraction of matrices depending on selection in switch-case construct and save it in the third empty matrix. and fourth nested loop for printing resultant array values as output.
This let’s you understand nested loop
[codesyntax lang=”c”]
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
scanf(“%d”,&A[I][J]);
}
}
[/codesyntax]
let’s understand selection in switch-case construct
[codesyntax lang=”c”]
printf("\nSELECT UR CHOICE (1.ADD 2.SUB 3.MULT) : ");
scanf("%d",&CH);
switch(CH)
{
case 1 :
{
if(M==R && N==S)
{
\\code for matrix addition
}
else
{
printf("\nERROR : CONDITION FOR ADDITION");
printf(" MATRICES IS NOT SATISFIED!");
}
break;
}
case 2 :
{
if(M==R && N==S)
{
\\code for matrix subtraction
}
else
{
printf("\nERROR : CONDITION FOR SUBTRACTION");
printf(" MATRICES IS NOT SATISFIED!");
}
break;
}
case 3 :
{
if(N==R)
{
\\code for matrix multiplication
}
else
{
printf("\nERROR : CONDITION FOR MULTIPLICATION");
printf(" MATRICES IS NOT SATISFIED!");
}
break;
}
default:
{
printf("YOU ENTERED WRONG CHOICE !!!");
}
}
[/codesyntax]
Condition for Addition or subtraction of two Matrices (matrix) : In order to add two matrices, A and B, the number of rows and columns in A must be equal to the number of rows and columns in B. Thus, if A is an m x n matrix and B is r x s matrix, m=r and n=s.
[codesyntax lang=”c”]
if(M==R && N==S)
{
\\code for matrix addition
}
else
{
printf("\nERROR : CONDITION FOR ADDITION");
printf(" MATRICES IS NOT SATISFIED!");
}
[/codesyntax]
Adding or subtraction two matrices is simple as we have to add or subtract all the elements of the first matrix with same row and column to the other matrix. The matrices can only be added or subtracted if the row and column is same.
[codesyntax lang=”c”]
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
C[I][J]=A[I][J]+(plus or minus)-B[I][J];
}
}
[/codesyntax]
Condition for Multiplication of two Matrices (matrix) : In order to multiply two matrices, A and B, the number of columns in A must be equal to the number of rows in B. Thus, if A is an m x n matrix and B is r x s matrix, n=r.
[codesyntax lang=”c”]
if(N==R)
{
\\code for matrix multiplication
}
else
{
printf("\nERROR : CONDITION FOR ADDITION");
printf(" MATRICES IS NOT SATISFIED!");
}
[/codesyntax]
Multiplication of two matrices is a bit complex as we have to do dot product of first row with first column multiply and add there product all the elements of the first matrix with row and other matrix with column. The matrices can only be added if the column of first matrix is equal to row of the second.
[codesyntax lang=”c”]
for(I=0;I<M;I++)
{
for(J=0;J<S;J++)
{
C[I][J]=0;
for(K=0;K<R;K++)
{
C[I][J]=C[I][J]+A[I][K]*B[K][J];
}
}
}
[/codesyntax]
Finally print the Numbers of Two Dimension Resultant Array in the Matrix form by using Tab (\t) and New Line (\n) character in the nested Loop at the end of the program.
[codesyntax lang=”c”]
for(I=0;I<M;I++)
{
for(J=0;J<S;J++)
{
printf(“%d\t”,C[I][J]);
}
printf(“\n”);
}
[/codesyntax]
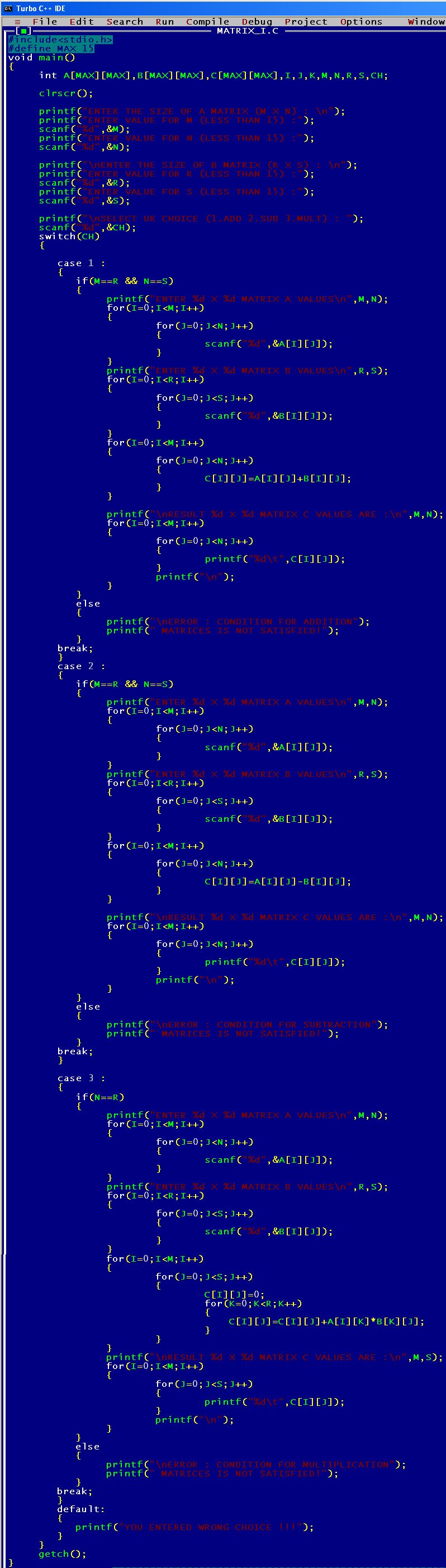
C program code :
[codesyntax lang=”c” lines=”normal”]
#include<stdio.h>
#define MAX 15
void main()
{
int A[MAX][MAX],B[MAX][MAX],C[MAX][MAX],I,J,K,M,N,R,S,CH;
clrscr();
printf("ENTER THE SIZE OF A MATRIX (M X N) : \n");
printf("ENTER VALUE FOR M (LESS THAN 15) :");
scanf("%d",&M);
printf("ENTER VALUE FOR N (LESS THAN 15) :");
scanf("%d",&N);
printf("\nENTER THE SIZE OF B MATRIX (R X S) : \n");
printf("ENTER VALUE FOR R (LESS THAN 15) :");
scanf("%d",&R);
printf("ENTER VALUE FOR S (LESS THAN 15) :");
scanf("%d",&S);
printf("\nSELECT UR CHOICE (1.ADD 2.SUB 3.MULT) : ");
scanf("%d",&CH);
switch(CH)
{
case 1 :
{
if(M==R && N==S)
{
printf("ENTER %d X %d MATRIX A VALUES\n",M,N);
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
scanf("%d",&A[I][J]);
}
}
printf("ENTER %d X %d MATRIX B VALUES\n",R,S);
for(I=0;I<R;I++)
{
for(J=0;J<S;J++)
{
scanf("%d",&B[I][J]);
}
}
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
C[I][J]=A[I][J]+B[I][J];
}
}
printf("\nRESULT %d X %d MATRIX C VALUES ARE :\n",M,N);
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
printf("%d\t",C[I][J]);
}
printf("\n");
}
}
else
{
printf("\nERROR : CONDITION FOR ADDITION");
printf(" MATRICES IS NOT SATISFIED!");
}
break;
}
case 2 :
{
if(M==R && N==S)
{
printf("ENTER %d X %d MATRIX A VALUES\n",M,N);
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
scanf("%d",&A[I][J]);
}
}
printf("ENTER %d X %d MATRIX B VALUES\n",R,S);
for(I=0;I<R;I++)
{
for(J=0;J<S;J++)
{
scanf("%d",&B[I][J]);
}
}
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
C[I][J]=A[I][J]-B[I][J];
}
}
printf("\nRESULT %d X %d MATRIX C VALUES ARE :\n",M,N);
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
printf("%d\t",C[I][J]);
}
printf("\n");
}
}
else
{
printf("\nERROR : CONDITION FOR SUBTRACTION");
printf(" MATRICES IS NOT SATISFIED!");
}
break;
}
case 3 :
{
if(N==R)
{
printf("ENTER %d X %d MATRIX A VALUES\n",M,N);
for(I=0;I<M;I++)
{
for(J=0;J<N;J++)
{
scanf("%d",&A[I][J]);
}
}
printf("ENTER %d X %d MATRIX B VALUES\n",R,S);
for(I=0;I<R;I++)
{
for(J=0;J<S;J++)
{
scanf("%d",&B[I][J]);
}
}
for(I=0;I<M;I++)
{
for(J=0;J<S;J++)
{
C[I][J]=0;
for(K=0;K<R;K++)
{
C[I][J]=C[I][J]+A[I][K]*B[K][J];
}
}
}
printf("\nRESULT %d X %d MATRIX C VALUES ARE :\n",M,S);
for(I=0;I<M;I++)
{
for(J=0;J<S;J++)
{
printf("%d\t",C[I][J]);
}
printf("\n");
}
}
else
{
printf("\nERROR : CONDITION FOR MULTIPLICATION");
printf(" MATRICES IS NOT SATISFIED!");
}
break;
}
default:
{
printf("YOU ENTERED WRONG CHOICE !!!");
}
}
getch();
}
[/codesyntax]
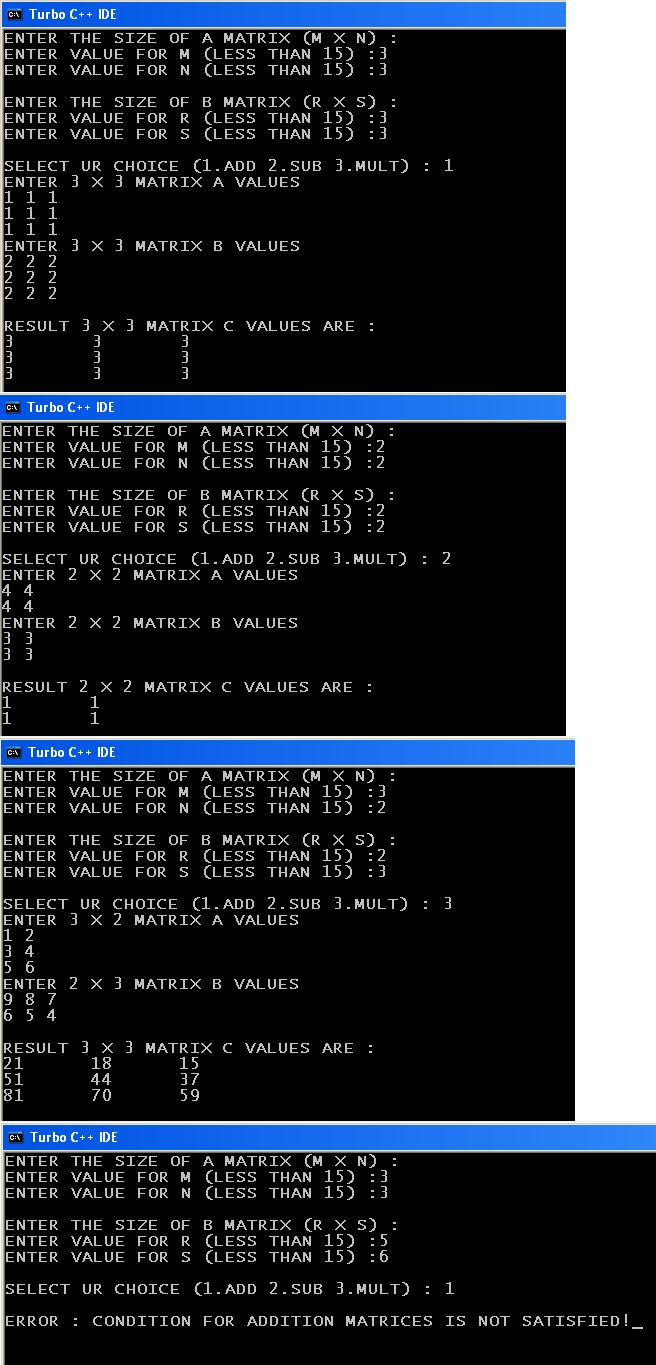
Note:- whenever you have large number of inputs to be entered, we can use space instead of enter button all the time. You can see have its done in Output screen.
SCREEN SHOTS:-
Note:- To understand program for sequence in detail Please SEARCH numerically example: C001, C002, etc.