Represent the following numbers in IEEE-754 floating point single precision number format: 4m Dec2005
(i) 1011.1001
(ii) -0.0011001
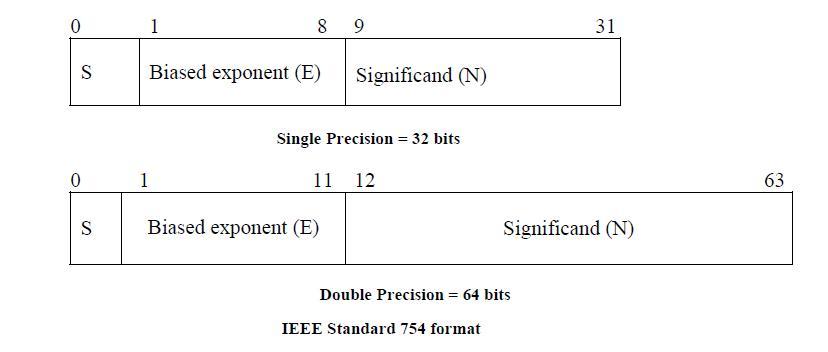
Single Precision
S stands for Sign (white color)
E stands for Exponent (yellow color)
N stands for Number (also called Mantissa or Significand) (green color)
0this Sign bit (1 bit)
1st to 8this Exponent bits (7 bits)
9thto 31this Exponent bits (24 bits)
Double Precision
S stands for Sign (white color)
E stands for Exponent (yellow color)
N stands for Number (also called Mantissa or Significand) (green color)
0this Sign bit (1 bit)
1st to 11this Exponent bits (10 bits)
12thto 63this Exponent bits (53 bits)
(i) 1011.1001
Since number is a positive number
Sign bit is: 0
| 0 |
Now let’s work on Mantissa part
First of all convert Binary number to Exponent Form
1011.1001 Will be 1.0111001 * 23
Discard 1.
Take 0111001 as Significand
Significand number = (0111001)2
Significand bits are:
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
Fill the Significand in the beginning
Rest all fills it with 0’s
We will have
Significand bits are:
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+3 is the Exponent
So we have to subtract it with 127
Exponent = 127+3=130
Exponent number (130)10 = (10000010)2
Discard overflow bit
Exponent bits are:
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
Note: we have to discard overflow bit since we have only 7 bits
(ii) -0.0011001
Since number is a negative number
Sign bit is: 1
| 1 |
Now let’s work on Mantissa part
First of all convert Binary number to Exponent Form
0.0011001 Will be 1.1001 * 2-3
Discard 1.
Take 1001 as Significand
Significand number = (1001)2
Significand bits are:
| 1 | 0 | 0 | 1 |
Fill the Significand in the beginning
Rest all fills it with 0’s
We will have
Significand bits are:
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
-3 is the Exponent
So we have to subtract it with 127
Exponent = 127-3=124
Exponent number (124)10 = (1111100)2
Exponent bits are:
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |