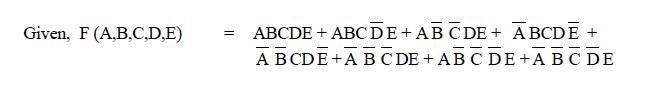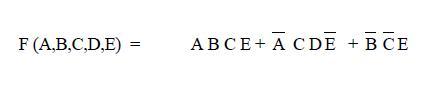Explain the basic principle of Quine-McCluskey method of simplifying the Boolean expression with the help of an example function. 6m Jun2007
Quine McKluskey Method
A tabular method was suggested to deal with the increasing number of variables known as Quine McKluskey Method. This method is suitable for programming and hence provides a tool for automating design in the form of minimizing Boolean expression.
The basic principle behind the Quine McKluskey Method is to remove the terms, which are redundant and can be obtained by other terms.
To understand Quine – Mc Kluskey method lets us see following example:-
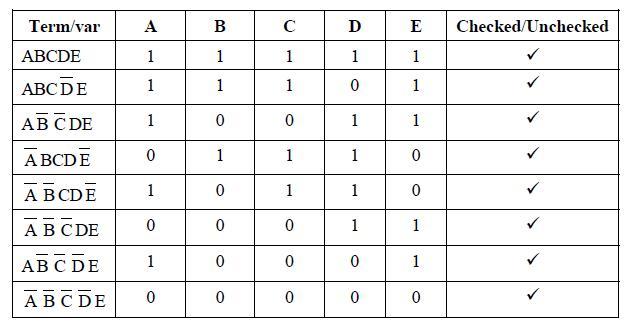
Step I: The terms of the function are placed in table as follows:
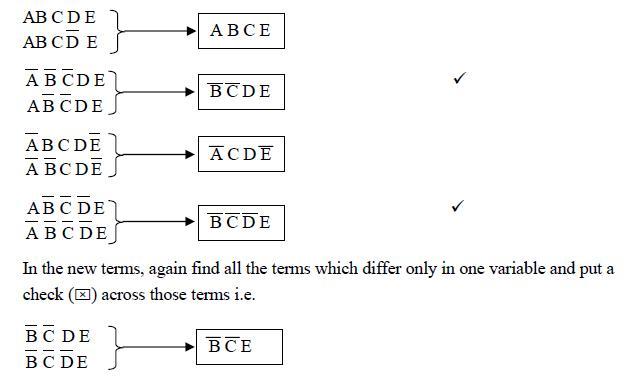
Step II: Forming the pairs which differ in only one variable also put check (v) against the terms selected and finding resultant terms as follows :-
Step III: Now, constructing final table as:
Thus all columns have mark ‘X’. Thus the final expression is:
The process can be summarized as follows:-
Step I: Build a table in which each term of the expression is represented in row (Expression should be in SOP form). The terms can be represented in the 0 (Complemented) or 1 (normal) form.
Step II: Check all the terms that differ in only one variable and then combine the pairs by removing the variable that differs in those terms. Thus a new table is formed. This process is repeated, if necessary, in the new table also until all uncommon terms are left i.e. no matches left in table.
Step III:
a) Finally, a two dimensional table is formed all terms which are not eliminated in the table form rows and all original terms form the column.
b) At each intersection of row and column where row term is subset of column term, an ‘X’ is placed.
Step IV:
a) Put a square around each ‘X’ which is alone in column
b) Put a circle around each ‘X’ in any row which contains a squared ‘X’
c) If every column has a squared or circled ‘X’ then the process is complete and the corresponding minimal expression is formed by all row terms which have marked Xs.
Design and draw the 4-bit adder-subtractor circuit using full adders and XOR gates. Explain its working in brief. 5m Jun2007
Solved Answer can be found on this link http://cssimplified.com/computer-organisation-and-assembly-language-programming/draw-the-logic-diagram-of-a-full-adder-create-a-2-bit-adder-subtractor-circuit-using-the-block-diagram-of-the-full-adder-6m-jun2007